复合材料RTM 工艺增强体的渗透性研究
复合材料树脂传递模塑技术(Resin Transfer Moulding , 简称RTM)是将液态热固性树脂及固化剂, 由计量设备(树脂泵)分别从储桶内抽出, 经静态混合器混合均匀后, 由注射枪注入事先铺有玻璃纤维增强材料的密封模内, 经固化、脱模、后加工而成制品的工艺方法 。RTM 工艺具有成型效率高, 原材料及能源消耗少, 设备和模具的投资少, 便于使用计算机辅助设计进行模具和产品设计, 成型过程中散发的挥发性物质很少, 有利于身体健康和环境保护 等优点, 因此被广泛应用于航空航天、汽车、电子电气、建筑、健身器材等领域, 在近几年更是得到了飞速发展。由于RTM 工艺发展时间较短, 不可避免地存在难关和有待进一步解决的问题。RTM 技术在国内外普遍存在的难点和问题主要表现在3 个方面
(1)树脂对纤维的浸渍不够理想, 制品里存在空隙率较高及干纤维的现象
(2)制品的纤维含量较低(一般为
(3)大面积、结构复杂的模具型腔内, 模塑过程中树脂的流动不均衡, 不能进行预测和控制。
渗透率是描述织物或增强体对树脂流动阻力的物理参数,可以用来表征树脂流过多孔介质玻璃纤维织物的难易程度, 它是孔隙率的函数。RTM 充模过程中, 精确描述树脂在增强体中的渗透特性, 对优化模具设计中的注入口和排气口位置、缩短制造周期、保证产品质量至关重要 。因此, 深入研究树脂在充模过程中对纤维的渗透性, 弄清其影响因素, 并做到能够设计、控制这些因素, 将会对RTM 的工业化进程产生巨大的推动力。
1 国内外对渗透性的研究现状
1.1 渗透模型的理论基础
流体流经多孔介质的理论有两条思路, 一是可以从统计的微观理论发展, 并指出如何导出一定的宏观定律;另一种途径是从由实验确定的经验定律出发, 这些定律一般为宏观定律, 如Darcy 定律。其基本假设是树脂流过预制件的过程相当于不可压缩流体通过多孔介质的过程。目前, 绝大多数研究人员将RTM 充模过程视为牛顿流体在多孔介质中的流动过程, 应用达西定律对其进行研究。
树脂在织物内的流动服从Darcy 定律, 将之写成理论公式为
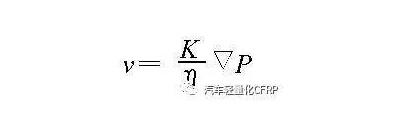
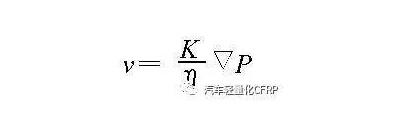
式中, v 是速度矢量, K 是渗透率张量, η是液体粘度, P 是压力梯度。
由于RTM 制件多为薄壁件, 厚度方向的尺寸与平面相比要小得多, 所以将树脂在织物内的流动简化为二维流动, 此时式
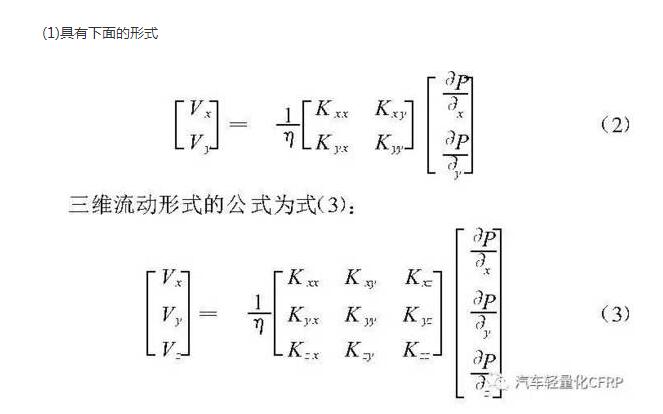

渗透率的表征方法
1.2.1 实验测量法
实验测量法主要是将不同类型的纤维和预成型体铺在模具内, 然后用已知黏度的流体, 通过记录成型过程的压力、流量等参数, 结合达西定律, 计算出预制件的渗透率。实验法测量渗透率是较为基础的一种方法, 可操作性较强, 不过要想得到可靠的数据需要进行大量的试验, 且对于不同预成型体渗透率的测试技术和测试方法尚未形成一个统一的标准。
常用的渗透率测定方法可分为两大类 , 第1 类是单向饱和流动法(简称单向法), 是在长方形(测面内渗透率)或圆柱状(测面外渗透率)模腔内, 测量恒定流速的树脂在已饱和的纤维体内的一维流动压力降, 代入达西定律, 即可得主渗透率。
单向法测量渗透率用到了达西定律3 种表达式中的一维形式。国内外测量的方法包括初级方法, 其基本原理是通过测量每一点的瞬时渗透率, 后算出瞬时渗透率的平均值就是所求的渗透率, 这种方法主要是针对设置较简单的点进行测试的方法。有学者用插值的方法求出树脂流动前沿的渗透率, 这种是实验所得的流动前沿中较适合的一种方法。还有用单点法即在实验中一点的位置测得渗透率。这种方法比较简单, 适用于注射长度较短或记录数据较少的情况, 否则将会有较大的误差 。
单向法的数据收集和处理比较简单, 通常适用于各向同性材料和横向正交各向异性材料, 但对后者不仅要分别测量两个主渗透方向, 而且事先要确定主渗透方向或进行反复试验确定,此过程比较繁琐, 且其结果易受边缘效应的影响。
第2 类测量法为径向流动法(简称径向法), 是通过透明上模观察和记录注射口在中心时, 树脂在恒定流速或恒定压力下对纤维体的浸润过程, 从树脂前沿的瞬时形状得出主渗透率的比值和主方向 ;同时用压力传感器测量注射口压力, 代入达西定律, 经过换算求出渗透率。
以上两种测量方法都主要是针对面内渗透率, 一般人认为面内两个方向的渗透率测量决定了整个充模质量。但是对存在树脂沿厚度方向渗透的情形, 如大型复合材料构件、RFI 制件,其厚度方向的渗透特性也需要进行研究。人为地将渗透率割裂为面内渗透率和厚度方向渗透率的做法, 不适用于真正意义上的三维结构预制件。因为对如编织、机织等三维结构织物而言,渗透率的主轴有可能偏离测量平面, 厚度方向上的有效渗透率并非渗透张量的第3 主渗透率。
有学者研究了树脂前沿形状和注射压力的关系, 发现在未浸润的三维织物中, 渐进的树脂前沿的毛细压力作用优于外加的注射压力, 树脂以毛细流动为主要流动形式, 不再符合达西定律的渗流条件 。为避免毛细作用的影响, 在国内有学者在一定的定型剂质量分数下, 测试流体在垂直方向上的流动基本为稳态流动, 大体受Darcy 定律控制
1.2.2 理论分析法
理论分析法就是根据液体在多孔介质中流动的机理, 建立一些分析模型来预测材料的渗透率。Ko zeny 在将纤维多孔介质中的纤维抽象成不可渗透的弯曲毛细管的基础上建立了一种解析模型, 即用毛细管模型来预测理想粒状介质的渗透率。这一模型提出后被广泛应用于描述复合材料加工中液体在纤维中的流动[ 10] 。Carmen 在此基础上引进一个水利半径的概念, 把毛细管半径和介质粒子半径联系起来, 使所有的参数为已知或可测量值, 提出了应用于单向纤维增强体渗透率预测的Kozeny-Ca rmen 公式。但Bruschke 的研究表明应用Kozeny-Carmen公式得到的渗透率值与实验结果有很大的偏差。这是由于毛细管模型的缺点是它不能模拟低孔隙率时横向流过纤维介质的渗透率。陈鹏等人在Koze ny-Ca rmen 公式的基础上建立了单向预成型体纵向渗透率的统计模型, 克服了以往渗透率模型不能反映预成型体渗透特性极限情况的缺点。以上这些研究都是以单向纤维为研究对象, 且试验中的参数也不易确定, 因此这些模型
的应用有较大的局限性。
规则排列柱阵模型是将纤维多孔材料看成规则排列的柱阵, 通过流体流经圆柱所受的拖引力, 计算纤维柱阵的渗透率。
这种模型存在两种极限情况, 在低孔隙率时, 柱体紧密堆积, 可用“ 近似润滑法” ;在高孔隙率时, 柱体间距增大, 这时可用“ 细胞模型” 。近似润滑法是把纤维看成紧密堆积的柱阵, 假设矩阵的一种可重复排列的方式, 针对其中的一个单元, 建立流体与柱阵间的空隙压降之间的关系。这种模型的不足之处是将纤维的排列理想化了, 在实际中纤维因复杂的结构和被挤压等因素,使得在用这种模型时将出现很大的误差。当孔隙率较高时纤维间的距离拉大, 包围纤维的流体间被认为不存在质量和能量的交换, 此时纤维排列方式也可忽略不计。Happel 和
先建立了纤维多孔介质渗透率预测的细胞模型。模型将纤维多孔介质考虑成同心圆柱, 中心圆柱为纤维, 外圆柱为流体。Happel 和Kuw abura 分别用不同的边界条件建立了模型的表达式, 经过一些学者的验证, 理论和试验的拟合度较好。以上研究都是针对各向同性规则排列纤维多孔介质的研究, 对于无规排列的各向异性介质只有少数学者进行了研究。
Sangani 和Yao 对无规排列纤维各向异性多孔介质沿纤维方向和垂直纤维方向的渗透率进行了预测, 研究结果表明纤维的这种无规排列会使渗透率比各向同性时增加两倍。Bruschke 和Advani 的研究提出了一种混合模型, 即在低孔隙率时应用近似润滑法, 高孔隙率时应用细胞模型, 具有一定的合理性。规则排列柱阵模型很好地解决了简单排列纤维多孔介质的渗透率理论预测问题。虽然这种方法对纤维束内的微观流动和纤维束间的宏观流动关系缺少研究, 但其理想化的几何模型还是成功地描述了简单纤维增强体的微观结构, 预测得到的渗透率值与实验数据具有较好的一致性。
1.2.3 数值模拟法
理论分析法建立了简化而确定的渗透率计算模型, 但都是以简单纤维排列的增强材料为研究对象。数值模拟法则常被用来分析流体在复杂孔隙结构预成型体中的流动行为, 并用来检验理论分析法的分析结果。树值分析法主要有3 种常用的方法:均匀化法、网格法和单胞法。
均匀化理论在许多复合材料工程问题中得到应用, 对求解具有周期性微观结构的问题十分有效 。将均匀化理论应用于多孔介质中的Stokes 流动, 可以建立预测渗透率的控制方程。戴福洪等 的研究将单向纤维看成具有周期性结构的多孔介质, 其研究从Stokes 方程出发将流体速度和压力展开为小参数的渐近级数, 由此得到渗透率预测的数学表达式。Takano等人的研究将均匀化理论应用于平面机织纤维渗透率的预测, 通过二维均匀化法将微观平面织物纤维构架和宏观材料渗
透率联系起来, 微观流动控制方程为Sto kes , 宏观流动控制方程为Dancy 定律。均匀化理论模型可以将复杂结构简化为一个简单的结构单元的研究, 同时它也可以分析外界因素导致的结构单元的变化对渗透率的影响。
Boltzman研究是在自由流体区应用Stokes 方程, 而在多孔介质区应用Bo ltzman 方程, 完成对流体力学方程的数值解法, 这就形成了多孔介质渗透率预测的Bo ltzman 网格法。这种方法可用于非稳态多向流体分析的优势将有可能被应用于树脂充模过程中微观孔隙的形成、生长和传递过程的分析, 这对充模过程的模拟是很有意义的。
纤维织物增强材料是纤维束按不同纺织工艺形成的具有一定几何构型的多孔介质材料, 当分析其微观物理性质时可将其小可重复特征单元从整体中分离出来定义为单胞, 并由此发展了渗透率预测的单胞法。这种单胞的明确定义能够更为直观和现实地反映纤维增强材料的微观几何构型, 使微观结构参数化。
国内学者也对RTM 充模过程做了数值模拟分析, 例如, 王继辉等人通过流体力学理论分析推导出达西定律的在各向异性介质中的三位流动的公式, 以此为基础, 建立有限元控制方程, 用于模拟RTM 的充模过程;梁志勇等人在普通
窗口下实现各类平面构件RTM 工艺过程的控制体积单元的有限元算法, 进行工艺过程的压力场及树脂流场模拟分析;张少春建立了RTM 充模过程的二维数学模拟, 用控制体积有限元法确定模拟RTM 充模过程中的树脂计算方法;吕昶等人利用数值模拟的方法, 分析RTM 工艺中的各种注射方式的充模过程;吴灵芝等人的研究在一定的实验数据基础上进一步讨论了非织造材料结构与渗透率之间的关系, 建立了非织造材料结构与渗透率之间的关系式。
2 RTM 工艺纤维渗透率的影响因素
2.1 纤维体积含量对渗透率的影响
模腔中的纤维体积含量对增强体的树脂渗透率有很大的影响。随着纤维体积含量的提高, 渗透率明显降低。同时纤维的体积含量或孔隙率对成型产品的质量也有很大影响。当纤维体积含量高或纤维孔隙率较低时, 纤维毡的结合更为紧密, 有利于模腔中气泡的排出, 可提高产品质量。另一方面, 纤维的体积含量增高或孔隙率较低时, 渗透率有明显降低, 将延长充模时间。因此, 纤维增强体的孔隙率存在一个佳值, 在此范围下纤维的浸润性达到佳状态 。
2.2 纤维层数对渗透率的影响
在其他条件不变的情况下, 纤维层数对纤维堆积状态影响较小, 压力一定时, 纤维体积分数基本不随层数变化。层数对平纹布的渗透率影响较大, 当纤维体积分数小于57%时, 随着层数的增加渗透率明显减小, 当纤维体积分数大于57 %时, 层数对渗透率的影响不明显;单向铺层和正交铺层时, 层数影响较小 。
2.3 纤维组织结构对渗透率的影响
在相同纤维体积含量的情况下, 不同结构的增强织物对渗透率也有影响。一些研究表明玻纤毡的渗透性要比玻纤方格布好得多 。其原因为, 虽然玻纤方格布纵横纤维束之间有的区域空隙很大, 但是两束纤维的交叠区域接触紧密, 渗透率明显下降, 且在成型过程中树脂很难完全浸透此区域, 影响复合材料制品的机械质量。而玻璃纤维毡的纤维束较细, 纵横向纤维在不同平面上, 没有像玻纤方格布那样有渗透率相差很大的区域, 因此纤维的渗透性较好。
2.4 缝合纱线对渗透率的影响
有学者通过数值模拟, 对缝合纱线对矩形纤维束间通道等效渗透系数的影响进行了定量研究。结果表明, 即使缝合纱线的尺度很小, 其存在也会对通道的等效渗透系数产生很大的影响, 因而在对有缝合纱线的纺织复合材料预制件进行有效渗透系数建模时, 缝合纱线的影响不可忽略。
2.5 树脂黏度对渗透性的影响
树脂黏度是影响渗透率和充模时间的关键因素之一。如果树脂黏度太大, 将致使注射压力高, 充模时间长, 树脂不易与纤维浸润, 模腔不易注满, 数值中夹带的空气不易去除;如果树脂黏度太小, 在充模过程中容易形成湍流, 并代入大量气泡, 响成品性能 。因此在测定的实验要求和实验环境下要确定适当的树脂黏度, 这样才有利于纤维的浸润和产品质量的保证。而树脂黏度在一定的范围内, 其对渗透率没有明显的影响。
2.6 成型温度对渗透性的影响
在RTM 充模过程中, 树脂在模腔内流动同时即开始固化。人们既希望固化时间缩短以提高效率, 又希望树脂能够充分浸润纤维。因此, 基本的要求是树脂在充完整个模腔后开始凝胶。注射成型温度会影响树脂的黏度、树脂的凝胶时间和纤维的表面张力。注射温度较低, 树脂的黏度增大, 树脂对纤维的浸润性变差。另一方面, 注射温度过高则会影响树脂的使用性能。
2.7 毛细压力对渗透率的影响
一些研究者认为毛细压力在渗透率的测试中是不可忽视的因素。从充模流动的机理来看, 流动可分为纤维束间的宏观流动和纤维束内的微观流动两种, 前者由充模压力控制, 后者主要受毛细作用的影响 。达西定律是由流体在已浸润的饱和介质内与外加压力下流动导出的, 而实际的充模过程是树脂流过干纤维束, 因此不可忽视毛细作用的影响。
2.8 真空辅助对渗透率的影响
真空条件下充模, 使得树脂易于进入孔隙, 并改善纤维的浸润效果。真空辅助可以显着减少RTM 工艺的气泡卷裹量 ,对增大产品的强度和减少空隙率提高渗透率有明显的作用。
3 结语
随着对渗透率研究的不断深入, 人们越来越意识到渗透率测试的复杂性, 对渗透率的研究有很多问题有待解决。到目前为止, 对渗透率影响因素大多处于定性分析阶段, 如何定量对其进行分析是一个重要的课题。单层结构是研究较早、建立模型较多的纤维增强材料, 但压缩形变对纤维体积含量的改变进而对渗透率的影响, 就很少有人提出理论分析模型;对于平面机织纤维厚度方向上的渗透率研究不够透彻;当存在多层增强体时,铺层方式的影响及流体在层间的流动规律还需深入研究;对于越来越多的被用来加工高性能纺织复合材料的缝合纤维预制件, 缝合纱线的存在对渗透性的影响的研究工作还很少;对于逐渐在航空航天和飞机制造业中广泛使用的三维纺织增强材料,很少有学者提出与其相关的渗透率预测模型;对增强材料的纤维含量的计算还不够系统、规范, 等等。此外, 建立我国渗透率数据库, 完善渗透率测量方法的标准化, 结合渗透率客观合理地将RTM 充模过程进行在线模拟分析, 从而对充模过程进行监测和控制将会对RTM 工业产生巨大的推动作用。
更多详细报道请关注复材网www.cnfrp.com








































