热压罐成形技术及关键数据提示
目前已经有大量的工作对热压罐成形复合材料工艺中发生的物理和化学过程进行模型化研究。在具体的制件和材料体系中, 这些模型为我们提供了理解这些复杂的物理化学变化和预测其固化工艺周期(包括压力、温度和真空度)的手段。在热压罐固化成形过程中发生的主要物理化学变化包括:①促进树脂的流动,使制件中的纤维被充分浸润和各层预浸料的准确到位;②纤维网络的压实,以使复合材料的纤维体积含量大化;③合适的压力以抑制树脂基体中空隙的形成;④合适的固化成形温度以保证树脂基体材料得到充分固化。
本文主要介绍了关于树脂的流动、纤维变形、压实模型、空隙形成、热传递和固化动力学等方面的进展。
1树脂的流动的模拟
为了充分模拟复合材料成形过程的压实行为,必须同时考虑树脂流动和纤维形变行为。当采用Darcy定律模型时,树脂在增强纤维中的流动被处理为在多孔介质中的流动,这个定律描述了流动速度依赖于使用的压力、流体黏度和纤维网络的渗透率。Darcy定律可以用如下矢量式来表述


在主轴上,只有对角线值(Kxx, Kyy, Kzz)为非零值。对于横向各向同性的单向层,这些方向分别对应于纤维轴向和两个相互垂直的横向轴。一般来说 ,纤维沿纤维方向的渗透大于横向和纤维厚度方向的渗透率。渗透率也是纤维体积含量、纤维半径和纤维结构的函数。通常情况下,渗透率只取决于材料参数和纤维体积含量,渗透率可以通过Kozeny Car- man方程表示式中:

K—— Kozeny常数 ;
rf——纤维半径 ;
k0值随纤维结构和流动方向而变化,已有报道,平行于纤维方向的k0值为0.5~ 0.7 ,而其横向流动的k0值常为11~ 18。Kozeny常数的测量值随实验条件的变化很大并且很敏感。事实上,当纤维体积含量接近它的理论极限时,纤维已经被迫在长度方向相互接触,其侧面或者厚度方向的流动可以忽略。Gutowski等在考虑了 停流现象后,对于横向渗透率提出了-一个可供选择的表达式式中:

V′a——横向流动已经停止时的纤维体积含量;
k'zz——修正的Kozeny常数。
从Gutowske等人的实验可以估测Va在0.76 ~ 0.82之间。
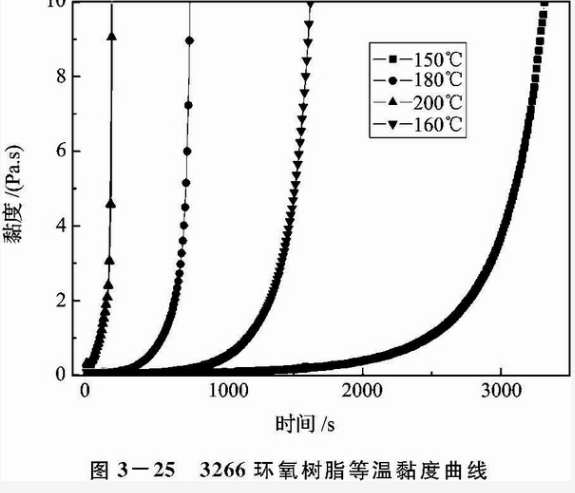
从式3-1可以看出,树脂的流动也依赖于树脂的黏度。大多数航空用预浸料的树脂呈”B” 阶或固态。因此,这些树脂的初始黏度比较高。当材料被加热时,黏度急剧下降,并在某一定温度范围达到较低值,这一定温度范围就是常说的热压罐成形周期中的"保温”温度,如图3一25中3266环氧树脂(北京航空材料研究院材料牌号)在160°C时的前900s。在该温度可确保增强材料完全被树脂浸透并有效地将多余的树脂挤入吸胶材料中。这段温度也是树脂容易形成空隙的温度,这时加在树脂上的压力是非常重要的。持续加热使树脂开始固化,树脂黏度的不断增加直到材料固化成形。热固性树脂在工艺过程中的状态变化很容易用时间一温度一转变曲线(TTT曲线)表达。通常,典型的环氧预浸料体系中的树脂,经过未凝 胶的玻璃区(冻胶态)到液体状态(黏度下降) ,然后经过凝胶反应(固化反应过程)并进入玻璃化状态(此时材料转变为固态)。
目前,有很多商业化的软件(如PAM- RTM)在已经知道渗透率的情况下进行流动前沿以及流动过程的模拟和分析,并用来指导模具设计和缺陷的控制。
2纤维形变
在复合材料热压罐成形过程中,当树脂的黏度很低时,树脂可能从预浸料中流出。实际上,对于有吸胶材料的成形过程,吸胶层会诱导树脂从预浸料中流入吸胶层,这一过程既确保了树脂的浸润,也有利于将空隙从复合材料中”排除” 。然而,一旦树脂从复合材料中流出,复合材料的纤维体积含量就被提高,这就减小纤维之间的间隙到纤维与纤维之间相互紧密接触的程度。当纤维之间的紧密接触达到一定程度后,纤维网络就将承载,并对复合材料中的所有流动行为产生了重要的影响。这一连串变化的重要的结果之一就 是树脂压力的减少,这可能导致树脂基体空隙的形成,终导致复合材料结构性能的下降。这些影响可以被包含在描述纤维束承载行为的压实模型中。对于横向压缩,这种关系可以通过使用压力和纤维体积含量之间的函数关系表达式中:

Va——可达到的大纤维体积含量;
V0——零载荷时的大纤维体积含量;
Β——描述纤维形状的常数。
这种模型已经在文献中得到了广泛的验证。
Springer就纤维形变、压实和固化模型等方面做了大量的工作。他认为复合材料被处理为由纤维层组成,而树脂通过这些纤维层流入吸胶材料。这个工艺过程中,假设复合材料的上层先被压实,然后逐渐压实渗透到底层,同时复合材料中多余的树脂被挤压出来。
后来,由Gutowski等研究了复合材料压实过程中纤维网络的形变模型。与Springer模型不同的是,Gutowski-Kardos的模型假设了纤维网络能够承受的一个有效载荷比例,尤其是在纤维体积含量较高的情况下。Gutowski- Kardos的模型将纤维 处理为一个弹性网络,而Springer模型则将纤维假设为具有众多接触点的梁,在压实过程中这些梁的跨距不断缩短,纤维网络的刚性也快速提高。
许多的研究者也建立了其他的模型和探索了这些理论的实验验证。在纤维体积含量小的情况下,Springer和Gutowski-Kardos的模型是基本等同的。但是,当继续压实复 合材料,树脂承受的压力可能大幅度地下降,纤维开始承受大部分的负荷,这时Gutowski- Kardos模型就显得更精确。
3压实模型
经过一定铺层的预浸料在热压罐成形的过程中,纤维将由 自然状态下进一步被压实,在这个过程中,树脂将在压实纤维中流动并传递流动压力。人们在这个过程中建立模型,研究树脂压力、渗透率和流动速率等之间的关系,来指导热压罐成形工艺。
在Springer提出的模型中,没有考虑纤维之间的接触。因此,模型认为树脂的压力与应用的工艺压力是相同的,这种压力驱动树脂依次穿过压实层进入吸胶层。求解问题包括确定树脂从复合材料流入吸胶层的边界压力条件。流体流动速率以渗透率和黏度的函数来表示,而且可以用它求解在连续条件下的压实模型方程。对于层合预浸料的吸胶层成形工艺(其中从复合材料中流出的树脂量必须等于流入吸胶胶层的边界压力条件。流体流动速率以渗透率和黏度的函数来表示,而且可以用它求解在连续条件下的压实模型方程。对于层合预浸料的吸胶层成形工艺(其中从复合材料中流出的树脂量必须等于流入吸胶材料的树脂量),Springer把复合材料厚度h的变化用以下方程

表示根据树脂黏度随时间变化的规律,可以计算每层的压实时间和层合板总的压实时间。这些过程分析为中低纤维体积含量的复合材料的厚度变化行为提供了一个合理的解释。
Gutowski- Kardos的分析考 虑到了伴随着树脂流动时的纤维网络的形变。这种方法与Springer的模型差异在于高纤维体积含量时,由于树脂流出,导致分配到纤维网络上的工艺压力也就有所不同。对于压实过程的分析, Gutowski- Kardos模型是从复 合材料元件厚度方向的形变与其三个主方向的诱导流动速率的关系入手的,当材料压缩时,Z方向上的单元就会变形。在Gutowski的分析中 ,这被处理为引入一个新的变量ξ,它是z坐标和原位变形w之和。因此,纤维的连续性可以表达如下

树脂流动连续性用下式表达
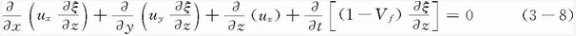
根据Darcy定律,与树脂压力Pr和纤维体积含量Vf相关的压实方程如下
.png)
结合纤维形变方程(方程3一9), 这个方程就可以形成给定时间和黏度的三维变化信息的压实全过程的数值化测定的基础。在热压罐成形过程中,树脂在三个主要方向都可能流动。然而由于大多数的制件相对它们宽度和长度来说很薄,所以穿过厚度方向的流动就占了主导地位,因此在z方向.上的一维流动就使人们更感兴趣。通过简化z方向流动方程(3-9) ,利用纤维承受的载荷a和引入新的变量e=(1-Vf)Nf,就可以得出Gutowski等人的结论。
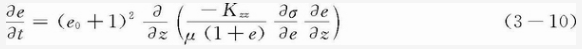
通过这个方程的数值求解,和等黏度油浸渍碳纤维实验获得的实验数据比较,其在Z方向上的流动比Carman-Kozeny方 程的预测更准确。








































